Page 24 - 2023年第54卷第7期

收敛因子 σ的大小，一般取较小的 σ ，例如 σ ＝ ０．０５甚至更小，同时增加迭代次数的控制值。

３ 不同数学模型的比较

［１］
以 Ｗｙｌｉｅ和 Ｓｔｒｅｅｔｅｒ 专著中的一个典型输水管中空气阀的水力瞬变为例，比较 Ｗｙｌｉｅ和 Ｓｔｒｅｅｔｅｒ空
气阀水力瞬变数学模型和本文新模型的差异。输水管长 １２１９．２ｍ，分成两段，Δ ｘ ＝ ６０９．６ｍ ；管径 Ｄ＝
２
０．６０９６ｍ ，对应截面积 Ａ ＝ ０．２９２ｍ ；水击波速 ａ ＝ １２１９．２ｍ?ｓ；达西 － 威斯巴哈沿程阻力系数ｆ ＝ ０．０２；
２
空气阀进排气通流面积 Ａ ＝ Ａ ＝ ０．００１８５８ｍ ，对应空气阀孔径 Ｄ ＝ ０．０４９ｍ ；空气阀安装在输水管中
ｉｎ ｏｕｔ ａ
间位置，管顶高程 Ｚ ＝ １０．３６ｍ；大气绝对压头 Ｈ ＝ ｐ? γ ＝ １０．３６ｍ；输水管下游是以一个水库作为边界
ａ ａ
３
条件，水位 Ｚ ＝ ９．７５ｍ；输水管进口处的强迫流量 Ｑ （１） ＝Ｑ － Δ Ｑｓｉｎ（ＯＭ× ｔ），Ｑ ＝ ０．３３９８ｍ ?ｓ，Δ Ｑ＝
０
０
０
Ｐ
３
０．１１３３ｍ ?ｓ，ＯＭ＝ ０．３ｒａｄ 。计算中取空气阀流量系数 Ｃ ＝ Ｃ ＝ ０．７ 。
ｉｎ ｏｕｔ
算例 １：当不考虑空气阀高度，包括检修阀和连接管高度，即 Ｚ ＝ Ｈ ＝ Ｚ，且取大气温度为 １０℃
ａｔ ｓ
和水温为 ４℃，即 Ｔ ＝ ２７３ ＋ １０ ＝ ２８３Ｋ和 Ｔ ＝ ２７３ ＋ ４ ＝ ２７７Ｋ ，则在气体为绝热流动 ｋ ＝ １．４ 条件下得如图
ａ
５所示空气阀水力瞬变的计算结果，图中：实线和虚线分别是新模型与 Ｗｙｌｉｅ和 Ｓｔｒｅｅｔｅｒ空气阀进排气
模型时水力瞬变的计算结果；Ｈ ＝ Ｈ － Ｚ为空气阀底部压头。
Ｐ
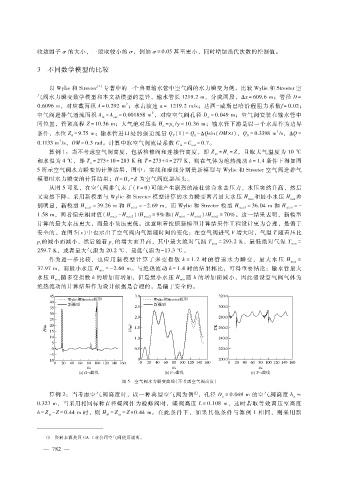
从图 ５可见，在空气阀排气未了（Ｖ ＝ ０ ）可能产生剧烈的液柱弥合水击压力，水压突然升高，然后
又突然下降。采用新模型与 Ｗｙｌｉｅ和 Ｓｔｒｅｅｔｅｒ模型计算的水力瞬变两者最大水压 Ｈ 和最小水压 Ｈ 差
ｍａｘ
ｍｉｎ
别明显，新模型 Ｈ ｍａｘ１ ＝ ３９．２６ｍ和 Ｈ ｍｉｎ１ ＝－ ２．６９ｍ ，而 Ｗｙｌｉｅ和 Ｓｔｒｅｅｔｅｒ模型 Ｈ ｍａｘ２ ＝ ３６．０４ｍ和 Ｈ ｍｉｎ２ ＝－
１．５８ｍ，两者偏差相对值（Ｈ － Ｈ ）?Ｈ ＝ ９％和（Ｈ － Ｈ ）?Ｈ ＝ ７０％。这一结果表明，新模型
ｍａｘ１ ｍａｘ２ ｍａｘ２ ｍｉｎ１ ｍｉｎ２ ｍｉｎ２
计算的最大水压更大，而最小负压更低。这意味着按照新模型计算结果作工程设计更为合理，是偏于
安全的。在图 ５（ｃ）中也示出了空气阀内气温随时间的变化：在空气阀进气 Ｖ增大时，气温 Ｔ随着压比
ｐ的减小而减小，然后随着 ｐ的增大而升高，其中最大绝对气温 Ｔ ＝ ２９３．２Ｋ 、最低绝对气温 Ｔ ＝
ｒ ｒ ｍａｘ ｍｉｎ
２５９．７Ｋ，或者最大气温为 ２０．２℃、最低气温为－ １３．３℃。
作为进一步比较，也 应 用 新 模 型 计 算 了 多 变 指 数 ｋ ＝ １．２时 的 管 道 水 力 瞬 变，最 大 水 压 Ｈ ｍａｘ ＝
３７．９７ｍ，而最小水压 Ｈ ＝－ ２．６０ｍ。与绝热流动 ｋ ＝ １．４时的结果相比，可得重要结论：输水管最大
ｍｉｎ
水压 Ｈ 随多变指数 ｋ的增加而增加，但是最小水压 Ｈ 随 ｋ的增加而减小，因此假设空气阀气体为
ｍａｘ ｍｉｎ
绝热流动的计算结果作为设计依据是合理的，是偏于安全的。

图 ５ 空气阀水力瞬变曲线（不考虑空气阀高度）

①
算例 ２：当考虑空气阀高度时，以一种典型空气阀为例 ，孔径 Ｄ ＝ ０．０４９ｍ的空气阀高度 ｈ≈
ａ
ａ
０．３２７ｍ，当采用相同标称直径蝶阀作为检修阀时，蝶阀高度 Ｌ ＝ ０．１０８ｍ ，这时若取等效调压室高度
ｈ ＝ Ｚ － Ｚ ＝ ０．４４ｍ时，则 Ｈ ＝ Ｚ ＝ Ｚ ＋ ０．４４ｍ。在此条件下，如果其他条件与算例 １相同，则采用新
ａｔ ｓ０ ａｔ

① 资料来源美国 ＧＡ工业公司空气阀使用说明。
２
— ７ ８ —