Page 15 - 2023年第54卷第8期

大量的研究，最终得到的结果形式均是在托马断面公式的基础上加以改进，并乘以一个安全系数，而
关于安全系数是否应该大于 １还是小于 １的讨论则一直延续至今。Ｓｃｈｕｌｌｅｒ、Ｋａｒａｓ、Ｆｒａｎｋ、Ｊａｅｇｅｒ、季
奎等人针对实际运行时调压室水位可能产生的扰动范围 ［３ － ４］ ，建议安全系数大于 １．０，最大可达到 ２．０；
董兴林、索丽生、孔昭年、杨开林等人考虑了调速器调节方式的影响 ［５ － ８］ ，Ｃａｌａｍｅ、Ｇａｒｄｅｎ、刘启钊、
杨建东、彭守拙、赖旭等人考虑了调压室底部流速水头及阻抗的影响 ［９ － １２］ ，均认为安全系数可小于
１．０；Ｓｃｉｍｅｍｉ在 ３个带调压室的水电站开展了现场试验，试验结果表明，３个调压室均不满足托马断
面，仍可稳定运行 ［１３］ ；刘丹总结了回龙山、太平哨两座面积远小于托马断面的调压室实际运行情况，
认为并网运行可以极大缩减托马断面 ［１４］ ；１９５７年，Ｃｈｅｖａｌｉｅｒ和 Ｈｕｇ分析了 Ｃｏｒｄｅａｃ水电站的试验结
果，认为调速器不可能保持出力不变，而是滞后 ２０ｓ左右，并提出了 “亚托马断面（ｓｕｂ － ＴｈｏｍａＳｅｃ
ｔｉｏｎ ）” 概念 ［１３］ ；Ｅｖａｎｇｅｌｉｓｔｉ与 Ｇｒａｄｅｌ分别考虑了水轮机效率对托马断面的影响，认为安全系数由水轮
机运行工况点的实际位置决定，大小在 １左右 ［１３］ ；我国水电站调压室设计规范推荐的安全系数在 １．０～
１．１之间，如小于 １．０，则需要进行运行稳定性与调节品质分析 ［１５ － １６］ 。近年来，随着溪洛渡、白鹤滩等
巨型水电站的陆续运行，在水机电一体化的基础上共同开展调压室稳定性问题的研究，已成为未来研
究的发展趋势 ［１７］ 。
本次研究在前人成果基础上，仍采用托马断面推导过程中的假设，不同之处在于将托马公式推导
过程中忽略的调压室后压力管道与机组后尾水道水体惯性重新予以考虑，进行结果对比，讨论托马公
式的合理性。

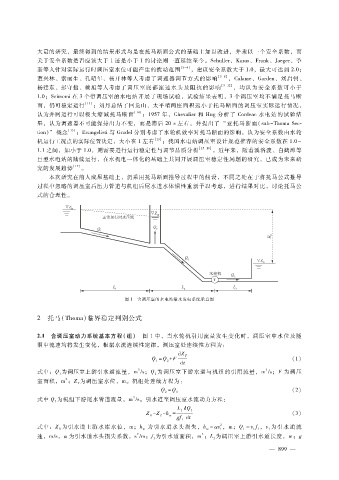
图 １ 含调压室的水电站输水发电系统示意图

２ 托马（Ｔｈｏｍａ）临界稳定判别公式

２．１ 含调压室动力系统基本方程（组） 图 １中，当水轮机引用流量发生变化时，调压室中水位及隧
洞中流速均将发生变化，根据水流连续性定律，调压室处连续性方程为：
ｄＺ Ｔ
Ｑ ＝ Ｑ ＋ Ｆ （１）
２
１
ｄｔ
３
３
式中：Ｑ为调压室上游引水道流量，ｍ ?ｓ；Ｑ 为调压室下游水道与机组的引用流量，ｍ ?ｓ；Ｆ为调压
２
１
２
室面积，ｍ ；Ｚ为调压室水位，ｍ。机组处连续方程为：
Ｔ
Ｑ ＝ Ｑ ３ （２）
２
３
式中 Ｑ为机组下游尾水管道流量，ｍ ?ｓ。引水道至调压室水流动力方程：
３
ＬｄＱ １
１
Ｚ － Ｚ － ｈ ＝ （３）
Ｕ Ｔ ｗ
ｇｆ ｄｔ
１
２
式中：Ｚ 为引水道上游水库水位，ｍ；ｈ 为引水道水头损失，ｈ ＝ α ｖ，ｍ；Ｑ ＝ ｖｆ，ｖ为引水道流
Ｕ ｗ ｗ １ １ １ １ １
２
２
速，ｍ?ｓ，α为引水道水头损失系数，ｓ?ｍ；ｆ为引水道面积，ｍ ；Ｌ为调压室上游引水道长度，ｍ；ｇ
１
１
— ８ ９ ９ —