Page 68 - 2024年第55卷第3期

幅提前等因素，本研究将每年 ７月至次年 ６月作为水
文年，鄱阳湖每年 ９月至次年 ３月作为枯水期。
选择基流指数（ ＢａｓｅＦｌｏｗＩｎｄｅｘ，ＢＦＩ）分割法 ［２２］
Ｉｎ
进行入湖基流分割得到 ＢＦ 。ＢＦＩ法的工作原理为：
ｔ
预设划分每个水文年的单位时段长，记为 Ｎ（天），将
年内径流过程划分为 ３６５?Ｎ个时段，每段最小值乘以
拐点检验因子 ０．９ ［２３］ ，当乘积小于等于相邻时段最小
值时，则认 为 是 一 个 拐 点， 重 复 操 作，选 出 其 它 拐
点，将拐点连接下方面积即为基流量。ＢＦＩ随 Ｎ增大
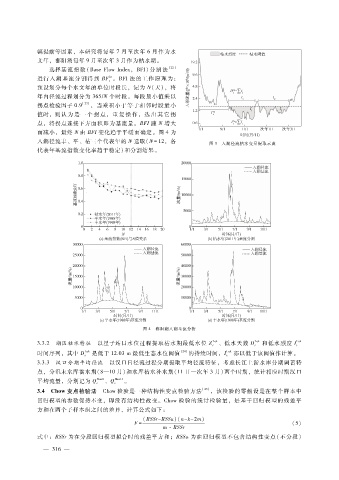
而减小，最终 Ｎ由 ＢＦＩ变化趋于平缓而确定。图 ４为
入湖径流丰、平、枯三个代表年的 Ｎ选取（Ｎ ＝ １２ ，各
图 ３ 入湖径流枯水变量提取示意
代表年基流指数变化率趋于稳定）和分割结果。

图 ４ 鄱阳湖入湖基流分析
Ｌａｋ
Ｌａｋ
３．３．２ 湖区枯水特征 以星子站日水位过程提取枯水期最低水位 Ｚ 、低水天数 Ｄ Ｌａｋ 和低水烈度 Ｉ
ｔ
ｔ
ｔ
Ｌａｋ
时间序列，其中 Ｄ Ｌａｋ 是低于 １２．０３ｍ最低生态水位阈值 ［２４］ 的持续时间，Ｉ 亦以低于该阈值作计算。
ｔ ｔ
３．３．３ 汉口分期平均径流 以汉口日径流过程分期提取平均径流特征，考虑长江上游水库分期调蓄特
点，分汛末水库蓄水期（８—１０月）和水库枯水补水期（１１日—次年 ３月）两个时期，统计相应时期汉口
平均流量，分别记为 Ｑ Ｈａｎ８ 、Ｑ Ｈａｎ１１ 。
ｔ ｔ
３．４ Ｃｈｏｗ变点检验法 Ｃｈｏｗ检验是一种结构性变点检验方法 ［２５］ ，该检验的零假设是在整个样本中
回归模型的参数保持不变，即没有结构性改变。Ｃｈｏｗ检验的统计检验量，是基于回归模型的残差平
方和在两个子样本组之间的差异，计算公式如下：
（ＲＳＳｒ － ＲＳＳｕ）（ｎ － ｋ － ２ｍ）
Ｆ ＝ （５）
ｍ·ＲＳＳｒ
式中：ＲＳＳｒ为在分段回归模型拟合时的残差平方和；ＲＳＳｕ为在回归模型不包含结构性变点（不分段）

６
— ３ １ —